Being a guide to portrait photography cleverly masquerading as a technical analysis

Like the topics we covered in the beginner’s guide last month, depth of field might initially seem complex, but behind it is some relatively simple logic and maths. Don’t worry if maths isn’t your strong point: long equations are the crutch of the inarticulate, and there’s nothing in this article more complicated than division.

Speaking of division, I like to divide photography into two broad disciplines. Portraits are photos of a particular object (not necessarily a person), designed to capture something about that object. Landscapes are photos of a scene (not necessarily outdoors), designed to capture the sensation of being in a place. I say that this is a disguised guide to portrait photography because mastering depth of field is one of the main skills you need to take great portraits. Whether you’re keeping the whole scene in focus for an environmental portrait, or using a very shallow depth of field to emphasise just the eyes of your subject, you need to understand how to get exactly the right depth.

Depth of field terminology

The following image depicts a (fake) flower about 50cm away, with a hedge around 5 meters behind it. This is an example of narrow depth of field: notice how some of the petals are sharp, others are slightly soft, and the hedge is almost blurred out of all recognition. Below it is a version with very wide depth of field.

Depth of field

The range of distances in a photo within which the image appears sharp. In this photo the sharp region starts about 49cm from the camera lens and extends to 51cm, giving a depth of field of 2 cm. Any point outside of this range appears blurred into a disc.

Blur

The size of the blur discs as measured in the real world. This is tied to depth of field: the larger the blur, the narrower the depth of field.

Circles of confusion

The size of the blur as measured on the photographic image.

Blur vs circles of confusion: Consider the rightmost petal and the leaves in the bottom right. The blur – measured in the real world – is around 2mm and 20cm respectively, and the circles of confusion – measured on the image – are around half a millimetre and 5mm respectively. When measured in the real world the leaves are 100 times more blurred than the petals, but measured on the actual photo they are only 10 times more blurred. This is because of perspective: the leaves are 10 times further away from the camera than the petals are, so the ratio of the two kinds of blur are different by a factor of 10.

I just measured those circles of confusion by counting pixels in the above image. This is valid, but inconvenient because the values would change if I altered the size of the image. For this reason, circles of confusion are usually measured on the camera’s sensor.

Over the rest of this article I’ll explain the physics behind blur and sharpness, so that you can learn to precisely control the look of your photos. An explanation of depth of field often starts with a list of rules. These do exist, and I list them at the end of the article, but the whole premise of a Geek’s Guide is that the rules are easier to learn if you understand the mechanism behind them first.

Onwards…

What causes blur in a photo?

First of all, consider a pinhole camera with no focusing capability and infinite depth of field:

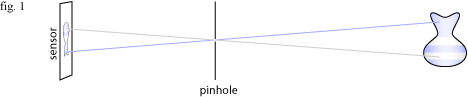
Light from each point in the scene enters the pinhole, forming an upside-down image on the sensor. Unfortunately, the vast majority of the light is wasted. Each point on the vase is emitting light in every direction, but only the light that happens to be emitted exactly in the direction of the pinhole will be captured. So little light comes in through the pinhole that you need long shutter speeds to expose the image. Also the small pinhole creates a very soft image due to diffraction. In order to allow more light in, the pinhole is replaced by a wide aperture and a glass lens to bend the light so that it still forms a sharp image on the sensor:

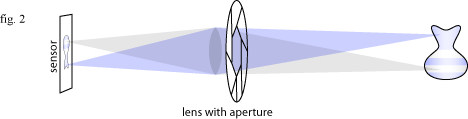
The lens works by bending light so that the rays emitted from any point on the subject have a larger target to hit, but still form a sharp image on the sensor. So far so good, but there is a cost. In the pinhole camera, all objects are equally in focus. With the lens, the focus must be adjusted for a subject. You tell the lens how far away the subject is, and it will make sure that light radiating from that distance is brought back to a single point on the sensor. The slice of the world that is in focus is called the focal plane.

So what about objects that are not on this focal plane? Light rays from points on these other objects will still be bent back to a single point by the lens, this point will be slightly in front or behind the sensor. If the object is in front of the focal plane then the light rays will not have enough distance to converge; if the object is behind the focal plane the rays will converge before the sensor and cross over. Either way they appear in the image as a blurred disc the same shape as the aperture. This disc is called a circle of confusion.

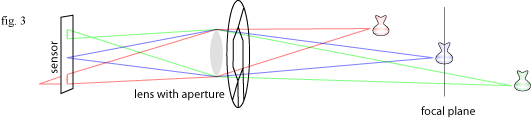
I find this model a bit hard to use to visualise the depth of field in a photo, but fortunately there is a much simpler one for predicting the size of the blur: imagine a pair of imaginary lines starting at the aperture and crossing over at the plane of focus. Any object not on the plane of focus will be blurred into a disc the size of the distance between the lines.

An example

This photo was taken with an 85mm lens at f/1.8, which means that it has an aperture width of 47mm.

The bottle is one meter from the camera, and half a meter behind the bottle are two candle flames which are blurred into discs.

According to the simple model above, since the candles are half as far from the focal plane as the camera is the circle of confusion should be half the aperture width, or 23.5mm. Measuring the discs in Photoshop, I find them to indeed be just over 23mm wide. Not bad.

The rule for calculating the blur according to the model in figure 4 is that if your subject is x meters away, an object that is x meters away from the subject will be blurred into a disc the size of the aperture, an object 2x meters behind the subject will be twice the size of the aperture, etc…

The size of the circle of confusion created by the candle flames is 2.14mm measured on the camera’s 35mm sensor.

Aperture shape and bokeh

Bokeh, pronounced with the ‘bo’ of ‘bombastic’ and the ‘keh’ of ‘Ken Livingstone’, is a term used to refer to the quality of the blur in the out of focus areas.

Circular bokeh is generally perceived to be the most pleasing. Any lens will produce circular bokeh when wide open, but when stopped down the bokeh takes on the polygonal shape of the aperture. Many people spend a lot of money on lenses that have great bokeh because they have wide apertures, are sharp even when wide open, and use many curved aperture blades to round out the polygonal shapes even when they are stopped down. Such people are called bokeh whores, and can be easily observed in their natural habitat of the flickr forums.

If one was so inclined, one could modify the shape of the aperture using a piece of card to produce any shape of bokeh you want:

Photo from a tutorial on DIY Photography.net, used with permission. More examples.

Obtaining sharp images

So far we’ve been talking about the size of the blur in the out of focus areas, now lets turn to the sharp area.

Firstly, we need a definition of what qualifies as ‘sharp’. Technically speaking, only the 2D slice of the world lying exactly on the plane of focus is perfectly sharp (and even then, only if the lens is a perfect optic, which it isn’t). However, since our eyes are even less perfect, we can use the more useful definition that a part of an image appears sharp when its resolution exceeds that of the human eye.

geeky aside: how to measure the size of the blur

So what is the resolution of the human eye?

In this image you can see a band crossing the flower petals and rising up the side of the vase in which everything seems to be sharp (it is clearer in the large version – click to open it). This is the range either side of the focal plane where the circles of confusion are so small that they appear as points.

How small do the circles have to be before they look like a single point? In an exhaustive analysis, Wikipedia tells me that assuming that you’re going to make 25cm wide prints and view them from a distance of 25cm, then you will perceive any circle less than 0.2mm wide as a single point.

This means that a circle of confusion must be no bigger than 1/1250 of the image width if the image is to appear sharp. This translates into a minimum circle of confusion of 1/1250^th of the sensor size. For 35mm cameras, the value 0.03mm is often used.

geeky aside: fact checking Wikipedia

Note that this is the minimum acceptable sharpness. If you’re a perfectionist or plan to make larger than A4 sized prints, you should strive to get your images even sharper.

Super sharp shooter shooting super super super sharp shots*

Most digital cameras are capable of greater resolutions than this 1/1250 of the image width, and just because you can’t see any resolution above 0.2mm from 25cm away, it doesn’t mean that any sharpness beyond that point is wasted. Firstly, you might want to print the image larger, or view it closer, than the values assumed above. Secondly, you may want to crop an image to enlarge a small portion of it. Finally, random visitors on flickr might pixel-peep your images on maximum magnification.

Here are some tips for obtaining images even sharper than ‘sharp’.

• Always use a tripod if possible, or alternatively a shuter speed of twice the normal recommendation of 1/<focal length>. e.g. for a 100mm lens, try and use a shutter speed of 1/200 second.
• By default, shoot at your lens’ sharpest aperture (typically f/8 or f/11 on SLR lenses) even if you don’t need all that depth of field. Especially avoid shooting wide open with cheap lenses: budget lenses tend to improve greatly when closed down 2 stops
• When using hyperfocal focussing (more on this later), double the recommendation of your depth of field calculations: if you reckon you need f/5.6 to get a sharp image, use f/11
• Avoid f-numbers higher than f/16: diffraction will degrade the image quality.
• Where the two previous rules contradict, consider recomposing the shot so that it doesn’t require quite so much depth of field, or using focus stacking (see the last section of this article)

* obscure British drum and bass reference

Visualising the depth of field

It’s imaginary line time again. Picture a cone extending from your lens to infinity, always 1/1250th the width of your image. I’ll call this the sharpness cone because as far as I know there’s no accepted name for it. If the blur discs are smaller than this cone, the image appears sharp. Using a 24mm lens which has a 72 degree angle of view on a full frame DSLR, this cone will be around a millimetre wide one meter from the camera, and a meter wide one kilometre from the camera.

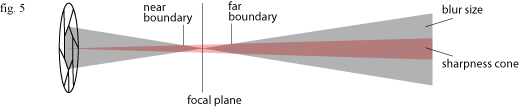
Between the near and far boundaries where the blur is smaller than the sharpness cone, the image will be perceived as sharp. The distance between the two boundaries is the depth of field.

Calculating the size of the depth of field

There are equations for calculating the near and far boundaries, which I shall include here even though I don’t fully understand them so that we may share a sigh of relief when I introduce a nifty gadget that calculates them for you:

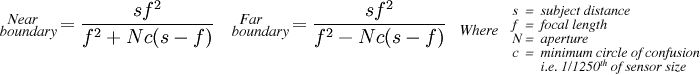
Yuck. Since pausing for a minute to use a calculator interrupts the creative process a bit, people use depth of field charts. I might not fully understand the above equation, but I can count that it has 4 variables. A single chart applies to one combination of focal length (f) and sensor size (c), leaving two variables left: subject distance (s) and aperture (N). The chart is a grid of the result of the above equations for every permutation of subject distance and aperture.

Go generate charts for all your lenses here: www.dofmaster.com/doftable.html. You use the chart by finding the row representing the subject distance, then selecting an aperture from that row that gives you the depth of field you need.

If you look at the bottom row of these charts, you will see that they have a figure for each f-number called hyperfocal distance.

Hyperfocal distance

Sometimes, especially during landscape photography, you want the whole of a scene to be in focus. In order to do this you use hyperfocal distance focussing. This can be explained in terms of concepts already covered in this article: the hyperfocal distance is the closest distance you can focus on at which the blur discs behind the plane of focus are always smaller than the sharpness cone. In other words, the red and grey lines in figure 5 never cross over and there is no far focus boundary: very distant objects are in sharp focus.

When you are focussed on the hyperfocal distance, everything from half that distance to infinity will be sharp. For example, the hyperfocal distance for an 85mm lens at f/8 is 30 meters; focus on 30 meters and everything from 15 meters to infinity will be sharp.

Bear in mind when using hyperfocal focussing that it will produce “acceptably sharp” images according to the 1/1250^th rule. However, if you don’t actually need all that depth of field it is possible to get sharper images. If the subject you’re shooting with the 85mm lens is 100 meters and there is no foreground that needs to be sharp, just focus on the subject!

The aesthetics of depth of field

The effect of focal length and aperture on depth of field has been mentioned above but a picture, as they say, is worth a thousand words.

The effect of focal length

Assuming that you change position to keep the subject filling the frame, focal length does not affect depth of field. However, the perspective causes the image to look different.

Look at these two photos large (click them to view the large size). At first glance the 85mm one looks like it has a thinner depth of field, but in fact this is not the case: in both photos the sharp area is about two squares of tablecloth thick, just enough to get the petals and the leaf sharp. In the second shot the perspective compresses the scene, causing the same depth of field to take up less space on the image.

Likewise the flower in the background is just as blurred in the second shot, but the circles of confusion are larger because the flower is larger. If you resize the flowers to compensate for perspective, you can see that the blur is identical.

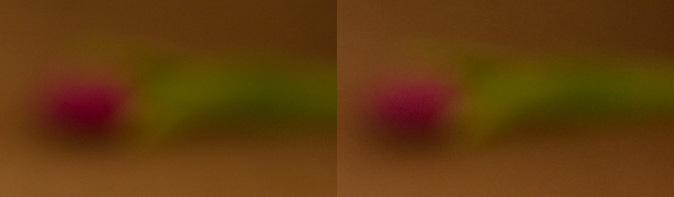
The effect of aperture

’nuff said.

The natural laws of depth of field…

There are some laws governing the relationship between these factors, which I shall call the Natural Laws of Depth of Field, highlighted in bold to convey an appropriate sense of gravitas. If you are one of those people who imagines the author speaking as they read an article, you may cast my voice in an “Ian McKellen as Gandalf” tone for this section.

Each of these rules explained in terms of the grey and red lines in figure 5, so here it is again for reference:

1. Larger apertures cause narrower depth of field

Increasing the size of the aperture increases the angle of the grey lines.

2. Closer subjects cause narrower depth of field

Bringing the subject closer to the lens increases the angle of the grey lines. Remember: Ian McKellen voice.

3. Cameras with larger sensors give more blur with a given focal length and f-number

This is a corollary of the previous rule: because full fame DSLRs have a wider angle of view than cropped DSLRs, you have to get closer to the subject to take the same picture with a particular lens.

The other way of looking at it is that with a full frame DSLR you have to use a longer focal length lens to get the same angle of view as a cropped DSLR, and that longer lens will have a physically larger aperture. Either way the effect is the same.

4. As long as your subject fills the frame, depth of field depends only on f-number, not focal length.

Increasing the focal length and then moving back to keep the subject filling the frame keeps depth of field and blur constant, but increases the size of the circles of confusion because of perspective. Increasing the focal length increases the physical size of the aperture, but at the same time you move backwards, so the angle of the grey lines in figure 5 does not change.

This is why telephoto lenses are good for background control in portraits: they make the background appear more blurred without sacrificing depth of field on the subject. (Also, because the telephoto lens includes less of the background, it is easier to select a less complicated bit of background for the composition)

5. Zooming in on a subject (increasing focal length while maintaining the same position) massively narrows the depth of field

Two effects combine to produce this: the longer focal length has a physically wider aperture (hence the angle of the grey lines in figure 5 becomes steeper) and the longer focal length magnifies the image (so the angle of the red lines becomes narrower)

some convoluted reasoning of questionable utility

… and how to break them

So now you know the rules of depth of field.

[Morpheus voice:] What you must understand is that these rules are no different than the rules of any computer system. Some of them can be bent, others can be broken.

Focus stacking

A technique called focus stacking can be used on macro photographs to increase the depth of field beyond the limits of optics. You take a series of exposures, changing the focal plane by a tiny amount each time so that every point on the subject is sharp in at least one exposure.

You then run the series of images through some software that generates a composite image made from the only the sharp parts of each image.

images copyright Charles Krebs, 2005, taken from heliconsoft.com.

Helicon Focus is commercial software that makes it very easy to create your own focus stacks. The best free program to do the same is probably CombineZM, and there are some more listed on Wikipedia.

Tilt-shift miniature fakes

If your aperture is big relative to your subject then you will get a narrow depth of field, and if not then you won’t. Since diffraction prevents you from having microscopically sized apertures, macro photographs have a narrow depth of field relative to the subject size. Likewise, since they don’t make lenses with apertures a meter wide, you won’t get a narrow depth of field when you shoot something the size of… well, a field.

This rule is so engrained in the minds of people who look at photographs that you can actually make a scene look like a tiny architectural model by adding fake depth of field. Your mind tells you that it must be small, because large subjects never have a narrow depth of field. This effect is called a ’tilt-shift miniature’, because it was first done using tilt shift lenses that can tilt their plane of focus to achieve this effect without digital processing.

First take an image shot from above. The higher the better, since you normally look down on a model. Then use a fake blur – for greatest realism a lens blur like the one in Photoshop – and selectively blur the regions behind and in front of an imaginary plane of focus. Here are some I found earlier, click on them to see the large versions:

Images by Dingo2494 and Photo Munki Deluxe on flickr. Hooray, for Creative Commons and for silly usernames.

The end!

That was my second photography article, I hope it was a better sequel to its predecessor than the Matrix Reloaded was. Feel free to post comments or ask questions below.